芝張りDIYですが、今回からちょっと番外編です。
皆さん、芝生に転圧がすごく重要だって知ってました?
どうやら転圧することで整地する効果に加えて、成長促進や密度が濃いターフをつくる効果があるそうです。
(ネットで検索するといっぱい出てくるので細かい説明は省略させて頂きます。)
ということで、せっかく丹精込めて芝生を育てるので転圧ローラーも掛けようと思ったんですが、調べてみるとかなり高額なんですよね。

学校用体育器具を取り扱っているようなメーカーのしっかりした商品だと10万円以上、

家庭用のチープなやつでも2万円くらいしちゃうんです。
それに、市販の廉価版のやつだと重量が90kg程度なんですが、あまり軽いと効果が薄いらしいので自分で自作することにしました^^
しかし転圧ローラーと言えば、

昔ながらの↑こんなやつをイメージしてましたが、今どきはメーカー品でも水や砂を入れるタイプのものに変わっているんですね。
すいません、導入部分から長くなってしまいましたが^^汗、
今回は転圧ローラーの設計というか、いろいろ物理的な考察をしてみたいと思います。
ローラーの大きさについて考察
まずはローラーをどれくらいの大きさにするか、そこから入っていきたいと思います^^
大前提として、業務用のカート式ローラーだとローラー部分だけで500kgくらいあるそうですが、
いくらローラーと言っても500kgもあったら人には引けないレベルなんじゃないかなと思います。
(一応、先程ご紹介したメーカー品のローラーが340kgだったのでその程度までなら人力でも引けるってことなんだと思いますが。)
で、人が操舵するのにどれくらいの重さなら無理なく引けるのか、その限界について調べてみました。
ある手押し運搬車のメーカーさんのホームページに
「手押し運搬車の積載荷重の限度は、路面や車輪径、タイヤ材質によって大きく影響されますが、最も多用されている汎用キャスタΦ180~200と平均的平路面では、300kg以下をお奨めします。」
と書いてありました^^
芝生の転圧に使用するのでタイヤの材質・路面については所与のものですが、車輪径に関しては大いに参考になりますね。
要するにトルクが重要ってことですが、
車軸にかかる走行トルク T=Fr×R は、半径R の増加に比例して大きくるため、車輪が大きいほどより大きな負荷に対応できるということですね^^
換言すれば、車輪が大きいほど同じ走行抵抗に対してより少ない力で押すことができるということになります。(経験則的に自転車もタイヤが大きい方が軽い力で漕げますもんね^^)
とっとは力には自信がありますが(体重が重いだけですが)、平路面ではなく土の上・芝生の上を転がすので、なるべく300kg以下で直径が大きくなる組み合わせが良さそうですね。
ということで、
作業性(ローラーを引いて何往復もすること)を考えて横幅は1mとして考えてみました。
(円柱にコンクリートを詰めるのでコンクリートの比重は2.3kg/㎥としています。)
- 直径200mmの場合
0.1m×0.1m×3.14×1m×2.3kg/㎥=72kg - 直径300mmの場合
0.15m×0.15m×3.14×1m×2.3kg/㎥=162kg - 直径400mmの場合
0.2m×0.2m×3.14×1m×2.3kg/㎥=289kg - 直径500mmの場合
0.25m×0.25m×3.14×1m×2.3kg/㎥=451kg
直径200mmだと72kgしかないので軽すぎるし土の上だと進まなそうな気もするので却下ですね。
直径300mmは162kgなので悪くはないですが、もう少し重くても良さそうですね。
直径400mmは289kgなので、うん!理想的ですね^^
直径500mmは重すぎて引っ張れるか分からないので却下です笑
ってことで直径400mmのローラーで行こうと思います^^
(直径500mmの場合は横幅を70cmくらいにすると丁度良さそうですね。往復の回数は増えますがトルクが効くのでもしかしたらこっちの方が良いかも知れません。)
一応、ネットで見ていると塩ビ管やボイド管なるものがあるそうで、ボイド管というのは↓こういうやつですね。

軸部についての考察
続いて、軸部についての考察です。
軸にするなら単管が安いので単管で良いかなと思ったんですが、直径400mmでいくと重量も300kgあるのでさすがに軸が単管だと摩擦抵抗で引っ張るのが重そうですよね・・・。
せっかく自作するのでベアリングとか入れて多少凝った感じのやつを作ってみたいですし笑
ってことで軸には全ネジを使おうかなと思ったんですが、ローラーも300kgありますからね・・・。
全ネジで300kgに耐えられるのか?
耐えられたとして、たわんで転がせなくなっちゃったりしないか?
とかいろいろ心配だったのでちょっと調べてみました。
たわみとか座屈の計算と言えばまず大事なのが断面二次モーメントですね^^
断面二次モーメントというのは「材料の曲げにくさ(曲げる力に対する抵抗性)」を表します。
要するに断面二次モーメントが大きいほど、曲げにくい材料と言えますね。
数式は以下の通り。

それではM20(という口径)の全ネジについて断面二次モーメントを調べてみましょう^^
全ネジはネジなので山と谷がありますが、保守的に谷の部分の直径17.294mmで計算してみると、
断面二次モーメントは4391mm^4、断面積234.90mm
という結果でした。
次にたわみの計算をしていきましょう^^
と言ってもとっとのブログは建築ブログではないので詳細は割愛させて頂きます。
(↓こんな感じの計算式を解くんですが、鋼のヤング率が205000N/mm^2でとかちょっと専門的になりすぎちゃいますからね笑)
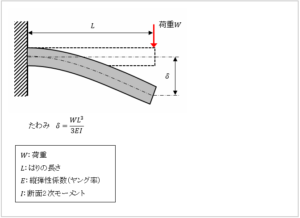
ということで結論ですが、
- 重さW=300kg、梁の長さL=10cmのときのたわみが1㎜程度
- 重さW=300kg、梁の長さL=20cmのときのたわみが9㎜程度
という結果になりました。
ローラーから突出した部分の梁の長さが20cmもあると9㎜もたわんじゃうのでダメですが、梁の長さは離れていても10cm程度だと思うので1㎜のたわみなら全然OKですね。
ちなみに梁の長さ10cmのときの最大応力は590MPaということなので、だいたい6トンくらいの重さまで破断せずに耐えられるということですから素材としては十分過ぎますね^^
結論、ローラー端部のベアリングから10cm以内の所で単管に繋げばOK。
ちなみに単管(Φ48.6mm、肉厚1.8mm)を軸にする場合は、
断面二次モーメントは38,372mm^4、断面積134.87mmですから断面積はM20の全ネジの方が大きいのに断面二次モーメントは単管の方が10倍も大きいという結果になります。
たわまない代わりに引くのは大変になりますけどね^^汗
ローラー端部に設置するベアリングの耐荷重に関しても一応調べてみましたが、1個で600kgくらいまで耐えられるようなので、ローラーの両端に設置することや、300kgのローラーを地面に置いて引っ張るということを考えると全然余裕ですね。
と、まぁ、大凡の物理的考察も出来たところで、あとはホームセンターにでも行ってみて実物を見ながら設計でも考えてみましょうかね^^
今回は計算ばっかりでさすがに疲れちゃったのでこの辺で終わりにしようと思います。


コメント